How to Tell if Graph is Continuous on the Domain

Domain of a Graph

Find the domain of a graph of a function; examples with solutions are presented. First the graphical meaning of the concept of the domain of a function is explained.

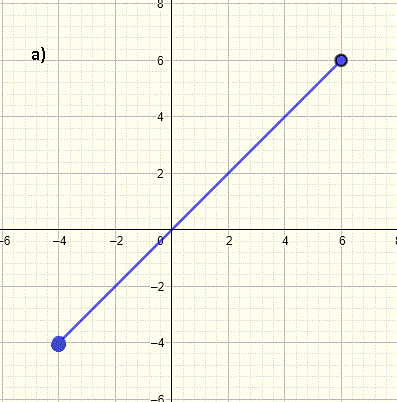
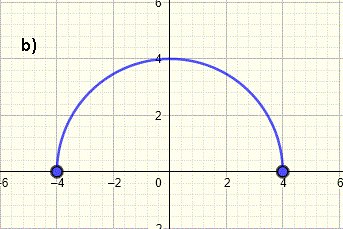
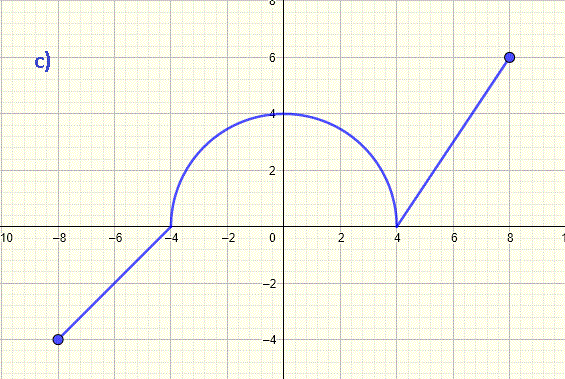
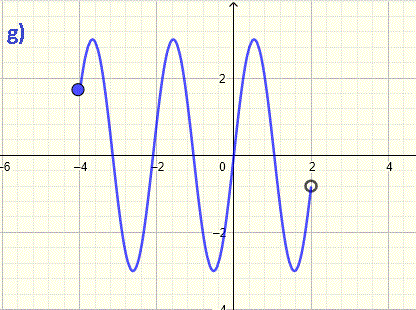
Domain of a Graph of a Function The implied domain of a function f is the set of all values of x for which f(x) is defined and real. The graph of a function f is the set of all points (x , f(x)). Hence, For a function f defined by its graph, the implied domain of f is the set of all the real values x along the x-axis for which there is a point on the given graph. As an example there are points on the graph below at x = - 3, - 2.5, -2, -0.5 , 2,5, 3, 3.2, 4. These values and more other values of x are included in the domain of f. There are no points on the graph at x = - 1 (open circle on the graph) , 0.5 , 1, 1.5 , 2 (open circle). These values and more other values of x are not included in the domain. With these ideas and definition, we will now solve examples where the whole domain of a given graph is found. Domain of a Graph; Examples with Detailed Solutions Example 1 Find the domain of the graph of the function shown below and write it in both interval and inequality notations. Solution to Example 1 The graph starts at x = - 4 and ends x = 6. For all x between -4 and 6, there points on the graph. Hence the domain, in interval notation, is written as [-4 , 6] In inequality notation, the domain is written as - 4 ≤ x ≤ 6 Note that we close the brackets of the interval because -4 and 6 are included in the domain which is indicated by the closed circles at x = - 4 and x = 6. Example 2 What is the domain, in interval notation, of the graph of the function shown below? Solution to Example 2 The graph starts at x = - 4 and ends x = 4. There are points on the graph for all values of x between - 4 and 4 including at - 4 and 4. Hence the domain, in interval notation, is written as [ - 4 , 4] Example 3 What is the domain of the graph of the function? Solution to Example 3 The graph starts at x = - 8 and ends x = 8. The graph is defined for all x between - 8 and 8. We include - 8 and 8 because of the closed circles at x = - 8 and x = 8. Hence the domain, in interval notation, is written as [ - 8 , 8] Example 4 Find the domain of the graph of the function shown below. Solution to Example 4 The graph starts at x = - 4 and ends x = 6. The graph is defined for all x between - 4 and 6. The interval is closed at - 4 and 6 because of the closed circles at x = - 4 and x = 6. Hence the domain, in interval notation is written as [- 4 , 6] Example 5 Write the domain of the graph of the function shown below in interval and inequality notations. Solution to Example 5 The graph starts at values of x > - 4 and ends at values of x < 4. x = - 4 and x = 4 are not included in the domain because of the open circles at these values. Hence the domain, in interval notation, is written as ( - 4 , 6 ) Note that the interval is open to indicate that - 4 and 4 are not included in the domain of the graph. In inequality notation, the same domain is given by - 4 < x < 6 Note that the strict inequality sign (without equal) is used in the inequality notation of the domain because x = - 4 and x = 6 are not included in the domain. Example 6 Write the domain of the graph of the function shown below in interval notation. Solution to Example 6 The graph starts at values of x = - 8 and ends at values of x < 2. The open circles at x = - 4, x = -2 and x = 2 indicates that these values are not included in the domain. Hence the domain, in interval notation, is written as [ - 8 , - 4 ) ∪ (- 4 , -2) ∪ (-2 , 2) Note the interval is open at x = - 4, x = -2 and x = 2 to indicate that these values are not included in the domain of the graph. Example 7 Write the domain of the graph of the function shown below in inequality notation. Solution to Example 7 The graph starts at x = - 4 and ends x < 2. The domain does not include x = 2 because of the open circle at x = 2. Hence the domain, in inequality notation, is written as - 4 ≤ x < 2 Example 8 Write the domain of the graph of the function shown below using interval notation Solution to Example 8 The graph is made up of three parts. The left part is defined for all values of x between - 4 and - 2. The part in the center is defined on the interval x > 0 and x ≤ 4. The part on the right is defined for x > 6 and x ≤ 6. The domain is written as a union of three intervals as follows [ - 4 , -2 ] ∪ (0 , 4] ∪ (6 , 8] More Links and References Find domain and range of functions, Find the domain of a function , Step by Step Solver to Find the Domain of the Square Root of a Linear Function, Find the Domain of the Square Root of a Quadratic Function

colegired1955.blogspot.com

Source: https://www.analyzemath.com/DomainRange/domain-of-a-graph.html

Share this post